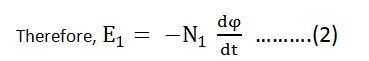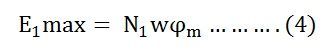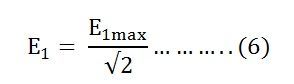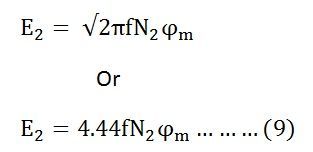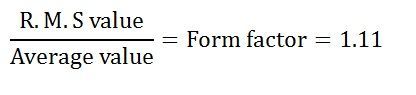When a sinusoidal voltage is applied to the primary winding of a transformer, alternating flux ϕ_m sets up in the iron core of the transformer. This sinusoidal flux links with both primary and secondary winding. The function of flux is a sine function.

The rate of change of flux with respect to time is derived mathematically.

The derivation of the EMF Equation of the transformer is shown below. Let

• ϕ_m be the maximum value of flux in Weber
• f be the supply frequency in Hz
• N₁ is the number of turns in the primary winding
• N₂ is the number of turns in the secondary winding

Φ is the flux per turn in Weber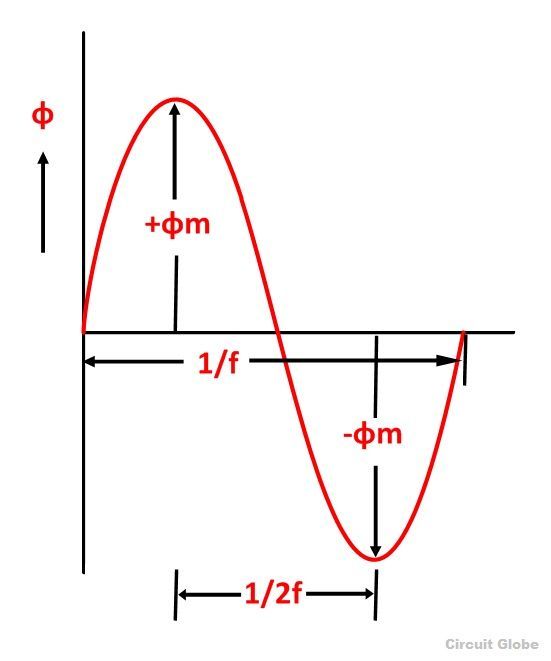
As shown in the above figure that the flux changes from + ϕ_m to – ϕ_m in half a cycle of 1/2f seconds.

By Faraday’s Law

Let E₁ be the emf induced in the primary winding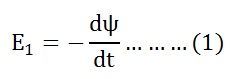

Where Ψ = N₁ϕ

Since ϕ is due to AC supply ϕ = ϕ_m Sinwt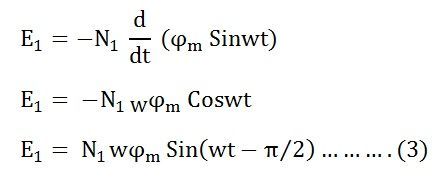

So the induced emf lags flux by 90 degrees.

Maximum valve of emf

But w = 2πf

Root mean square RMS value is

Putting the value of E₁max in equation (6) we get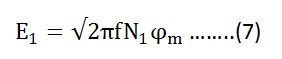

Putting the value of π = 3.14 in the equation (7) we will get the value of E₁ as

Similarly

Now, equating the equation (8) and (9) we get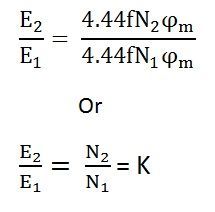

The above equation is called the turn ratio where K is known as the transformation ratio.

The equation (8) and (9) can also be written as shown below using the relation

(ϕm = B_m x A_i) where A_i is the iron area and B_m is the maximum value of flux density.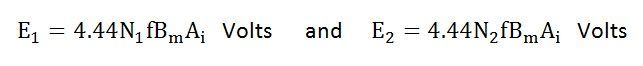

For a sinusoidal wave

Here 1.11 is the form factor.